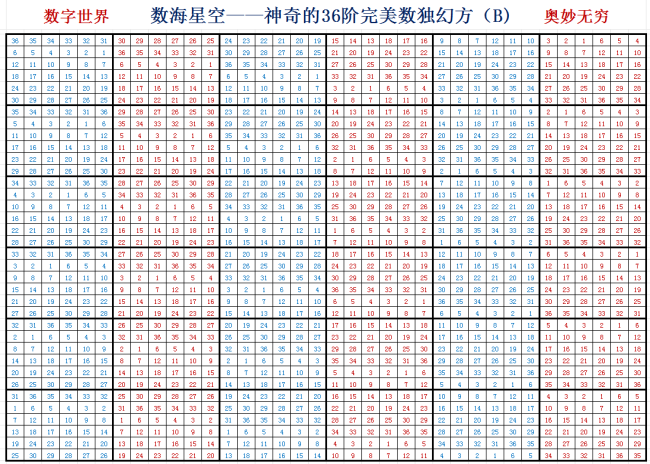
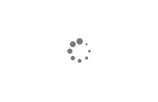——神奇的36阶完美数独幻方

  方有昆  何昌荣  

〔摘要〕完美数独幻方是数独的升华和发展，是数独的更高境界；是研究和探索珠算珠心算在数字科学领域中的神奇运用。

〔关键词〕  36阶完美数独幻方  36阶乘  6阶数学迷宫图   

珠算、珠心算  开发儿童智力  数字科学

完美数独幻方是数独的升华和发展，是数独的更高境界；是研究和探索珠算珠心算在数字科学领域中的神奇运用。数字世界、奥妙无穷, 此完美数独幻方图中的数字就像天上的星星各就各位，相互依存，其寓意深刻，令人赏心悦目。

一、A图、B图其共同特性如下：

1、每行36个数字，1至36不重复，和都等于666；

2、每列36个数字，1至36不重复，和都等于666；

3、毎条对角线36个数字，1至36不重复，和都等于666；

4、每个粗实线内6×6方阵36个数字，1至36不重复，和都等于666；

5、每个粗实线内“6×6”方阵中有36个格子，图中有36组“6×6”方阵，在每个方阵相同位置的小格子中各取一个数，共36个数字，1至36个数字不重复，和都等于666；

6、A图和B图中都内含了36组6阶数学迷宫图,每个粗实线内的“6×6”方阵,都是一组6阶数学迷宫图, 每组的迷宫图任选6个数，其和都等于111（备注：每行每列只能选一个数）。

（1）6阶数学迷宫图

例、选A图中第8组6×6方阵：  

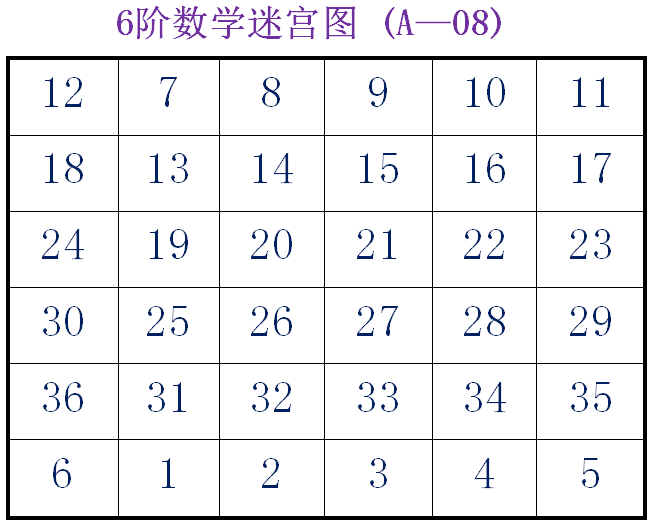
说明：任选6个数，但，都不能同行、同列 ,6个数之和都是111。

（2）数学迷宫图的奥妙:

1）无论哪一行插入任何一行都又是一组新的6阶数学迷宫图；

2）无论哪一列插入任何一列也都是一组新的6阶数学迷宫图。

7、A、B两组完美数独幻方图相互对应关联，如A图中每个粗实线“6×6”方阵中，相同数字的36个位置，其36个相同数字的位置在B图中就是不重复的1至36个数，数字之和都为666；反之B图中每个粗实线“6×6”方阵中，相同数字的36个位置，其36个相同数字的位置在A图中也是不重复的1至36个数，数字之和都为666；如A图中数字8的36个位置，在B图中就是1至36个数，其数字之都等于666；反之B图中数字8的36个位置，在A图中也是1至36的数，其数字之都等于666；以此类推其它35个数也同样如此。

     8、其他有规律的组合，1至36个数字不重复，和都等于666。

备注： 

     1、最大的亮点是：无论A图或B图只要将第一行1至36的数变化排列，以表中创编的方法，都可以编排出3.7×1041组（36阶乘），相同品位和高境界的36阶完美数独。

     2、以此方法，可以编排出N²阶多品位、高境界的完美数独幻方。

     完美数独幻方展示了数字世界的奥妙，36阶完美数独幻方及N²阶完美数独幻方是我们在研究珠算文化和珠心算教学中新的发现和创新，即可作为科研有关项目的参考，又可为开发儿童智力提供有效地帮助。

合肥市珠算心算协会

附:1、神奇的36阶完美数独幻方 （A）

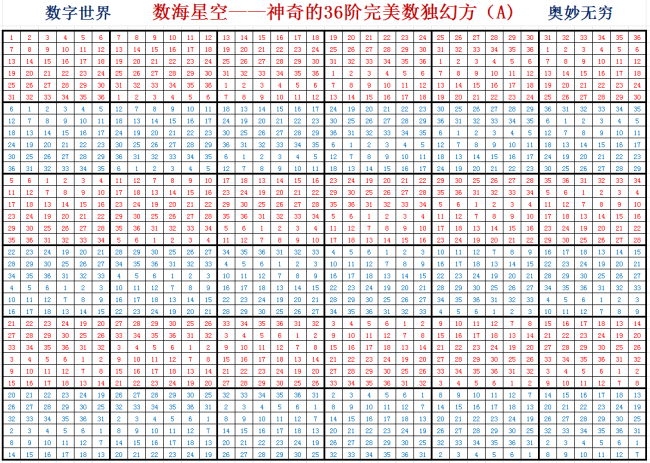
    2、神奇的36阶完美数独幻方 （B）